U Bajtoviji Đurica je odlučio da uvede struju. Spojio je n kuća pomoću m dalekovoda različitog kvaliteta. Za svaki dalekovod se zna posle koliko sati neodržavanja zarđa i prestaje da provodi struju. Ispostavilo se da bi, kad bi pustio mrežu u rad, došlo do kratkog spoja i velike katastrofe. Zato je Đurica uposlio Dragančeta da ispita mrežu. Draganče je ispostavio Đurici izveštaj, u kome se nalazi spisak k parova kuća koje ne smeju međusobno da budu spojene (ni direktno dalekovodom, ni preko drugih kuća) da bi mreža smela da se pusti u rad. Đurica može da bira koje dalekovode će da nastavi da održava, a koje ne. Đurica vas je uposlio da odredite koliko najmanje sati mora da prođe da bi mogao da pusti mrežu u rad, a Dragančeta za teži deo posla, da ispita koje dalekovode da održava, a koje ne, na osnovu vašeg izveštaja.

Ulaz:

U prvom redu ulazne datoteke struja.in nalazi se prirodni brojevi n, m i k (1 ≤ n, k ≤ 10000, 1 ≤ m ≤ 100 000). U sledećih m redova nalaze se po tri broja i, j, kv koja označavaju da su kuće i i j spojene dalekovodom kvaliteta kv (1 ≤ kv ≤ 1 000 000 000, posle kv sati prestaje da propušta struju ako se ne održava). Zatim se u preostalih k redova nalazi po dva broja i i j, koja označavaju da kuće i i j ne smeju biti spojene, da bi mreža smela da se pusti u rad. Nijedan par gradova nije spojen direktno više od jednim dalekovodom, ni 2 puta naveden na Dragančetovom spisku.

Izlaz:

U izlaznu datoteku struja.out upisati minimalan broj sati s koji mora da prođe da bi mreža smela da se pusti u rad.

Primer:

7 8 3
1 2 5
1 4 8
3 2 3
4 3 2
4 5 3
5 6 6
5 7 3
6 7 9
2 5
1 3
5 7

6

Objašnjenje:

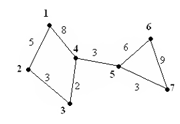
Opis dalekovoda iz ulaza odgovara dalekovodu prikazanom na slici iznad. Moguće je osposobiti mrežu za 6 sati, ako prestanu da se održavaju dalekovodi 1-2, 3-4, 5-6, 5-7

Prvo treba primetiti da je zadatak moguće rešiti tako što se ne održava nijedan dalekovod, i da je potrebno izračunati posle koliko sati dati parovi kuća neće biti spojeni. Takođe treba primetiti da je potrebno posmatrati samo one sate u kojima bar jedan od dalekovoda prestaje da propušta struju. Proveru da li je posle nekog konkretnog sata moguće pustiti mrežu u rad, je moguće uraditi pomoću nalaženja komponetni povezanosti (pomoću DFS-a ili BFS-a), i provere da li neki par kuća, koje ne smeju biti povezane, pripada istoj komponenti povezanosti. A pronalaženje odgovarajućeg broja sati je moguće binarnom pretragom, po svim mogućim satima.

Složenost binarne pretrage je O(log m), složenost nalaženja komponenti povezanosti O(m + n) (ako se graf čuva preko lista povezanosti), i provera parova O(k), pa je složenost algoritma O ((m + n + k) * log m).

Pseudokod

// sat - sortiran niz svih satova u kojima se kvari neki dalekovod
// sat[l] - najmanji, sat[d] - najveci
while (d-l>1)
{
    s=(l+d)/2;

    if (moze(sat[s])
       d=s;
    else
       l=s;          
}            
if (moze(sat[l]))   
   	d=l;

write(sat[d])


dfs(int i,int komp,int kv)
{
    ozn[i]=komp;
    int j;
    (za sve cvorove j povezane sa cvorom i granom veceg kvaliteta od kv)
       if (ozn[j]==0)
          dfs(j,komp,kv);
}
int moze(int s)
{
    (postavi sve ozn na 0)
    int i,komp=1;
    (za sve cvorove i)
       if (ozn[i]==0)
          dfs(i,komp,s);
    komp++;

    int ind=1;
    (za sve parove kuca kuca1 i kuca2, dok je ind==1)
         ind=(ozn[kuca1]!=ozn[kuca2]);

    return ind;	
}

#include <stdio.h>
#include <stdlib.h>
#include <memory.h>

const int maxn=41000;
const int maxm=110000;

typedef struct{
  int p,q,kv;
} grana;

int kuca1[maxm],kuca2[maxm],sat[maxm],poc[maxn],ozn[maxn];
grana pov[2*maxm];
int n,m,k;

int upG(const void *px,const void *py)
{
    grana *x=(grana *)px;   
    grana *y=(grana *)py;
    if ((x->p)>(y->p)) return 1;
    if ((x->p)<(y->p)) return -1;
    if ((x->kv)<(y->kv)) return 1;
    if ((x->kv)>(y->kv)) return -1;
    if ((x->q)>(y->q)) return 1;
    if ((x->q)<(y->q)) return -1;
    return 0;
}
int upI(const void *px,const void *py)
{
    int *x=(int *)px;   
    int *y=(int *)py;
    if (*x>*y) return 1;
    if (*x<*y) return -1;
    return 0;
}

void dfs(int i,int b,int s)
{
    ozn[i]=b;
    int j;
    for(j=poc[i];(j<poc[i+1]) && (pov[j].kv>s);j++)
       if (!ozn[pov[j].q])
          dfs(pov[j].q,b,s);
    return;      
}



int moze(int s)
{
    memset(ozn,0,sizeof(ozn));
    int i,j=1;
    for(i=0;i<n;i++)
       if (!ozn[i])
          {dfs(i,j,s);j++;}
       
    int ind=1;
    for(i=0;(i<k)&&ind;i++)
       ind=(ozn[kuca1[i]]!=ozn[kuca2[i]]);
    return ind;           
}

int main()
{
    freopen("struja.in","r",stdin);
    freopen("struja.out","w",stdout);

    int i,j,l,d,s;

    scanf("%d%d%d",&n,&m,&k);
    for(i=0;i<m;i++)
    {
       scanf("%d%d%d",&(pov[2*i].p),&(pov[2*i].q),&(pov[2*i].kv));             
       pov[2*i].p--;pov[2*i].q--;
       pov[2*i+1].p=pov[2*i].q;
       pov[2*i+1].q=pov[2*i].p;
       pov[2*i+1].kv=pov[2*i].kv;
       sat[i+1]=pov[2*i].kv;
    }
    for(i=0;i<k;i++)
    {
       scanf("%d%d",&(kuca1[i]),&(kuca2[i]));
       kuca1[i]--;kuca2[i]--;
    }
       
    qsort(pov,2*m,sizeof(grana),upG);
    for(i=j=0;i<=n;i++)
    {
        while ((pov[j].p<i) && (j<2*m)) j++;             
        poc[i]=j;
    }
    
    sat[0]=0;
    qsort(sat,m+1,sizeof(int),upI);    
    for(i=1,j=0;i<=m;i++)
    {
       if (sat[j]!=sat[i])
       {
          j++;
          sat[j]=sat[i];
       }     
    }
    
    l=0;d=j;    
    while (d-l>1)
    {
          s=(l+d)/2;
          if (moze(sat[s]))
             d=s;
          else
             l=s;          
    }            
    if (moze(sat[l]))   
       d=l;
    
    printf("%d\n",sat[d]);
    
  return 0;
}